When my teammates asked me to implement a math system, they asked me if it’d be possible for a designer to write out an expression like 2*(3+4) or -2+3*(4-5) or (2+3)-(3-5) – really, all they wanted was any arbitrary human-readable mathematical expressions to yield a final output. And when they described what they were looking for, I immediately thought about the HP 35S calculator.
Reverse Polish Notation

A photo of the HP 35S circa 1972 (image credit: HP Virtual Museum)
Aside from the fact that Hewlett Packard named its scientific calculator the 35S because it had 35 keys when it debuted, the really interesting note about the calculator is that it was built to compute any arbitrary human readable expression using an operational stack and Reverse Polish Notation.
First, let’s talk about what Reverse Polish Notation is, and why it was so useful in solving this problem for our designers. Reverse Polish Notation, or RPN, is the popular name for operator postfix notation in mathematics. Typically, we write mathematical expressions in a way that is easy for humans to read and understand. Take 2*(3+4) as an example – if we were to write that expression on a whiteboard and ask someone to solve it, it would be a simple task, because a person would know to first solve the parenthetical expression (3+4) before multiplying the result by 2 to arrive at the the final value of 14.
We use the phrase, “human readable” because a computer doesn’t know how to semantically evaluate and expression like a*(b+c) without some help. And this is where the invention of RPN comes to save the day.

Jan Łukasiewicz (Image credit: School of Mathematics and Statistics, University of St. Andrews, Scotland)
In the 1950’s, one of the most important mathematical logicians in modern history, Jan Łukasiewicz, published a book on formal logic, which includes demonstrations on how any arbitrary expression can be represented without its parentheses by placing operators before or after their operands. For example, a*(b+c) can be represented as *a+bc, which is better known as operator prefix notation because the operator precedes its operands or it can be represented as a*bc+, which is (you guessed it) operator postfix notation.
As a way of honoring the Polish-born logician and philosopher, operator prefix notation was popularly named Polish Notation and operator postfix notation was named Reverse Polish Notation. And if we were to semantically read the a*bc+ RPN expression like a computer would, we’d read the expression as “multiply a by the sum of b and c” – which is very useful when translating a designer’s infix notation (infix means that the operator is placed between its operands) to a data representation that a computer can use to read from and write to.
Which brings us back to the brilliance of the engineering that went into the HP 35S calculator. If you remember what we said about the 35S calculator, we mentioned that it was built to compute any arbitrary human readable expression using an operational stack and RPN. By now, you know all about RPN and if you think about it, RPN expressions like a*bc+ lend themselves quite nicely to one of the most widely and reliably used data structures in computer programming, the handy-dandy stack.
Stacks
Stacks are a great data structure – mostly because stacks appear in routines that span a wide range of use cases, including converting infix expressions to postfix. Now, if you’ve never heard of a stack – you’re missing out because it’s awesome. Technically, computer scientists label a stack as an abstract data type that has two main operations, pushes and pops, which is super elegant if you think about it in a real-world context.
For example, if you have a whole bunch of plates that need to be washed, you may want to follow the simple method of “pushing” the plates onto a large stack before “popping” them off one by one to wash them.

A stack of plates (Image Credit: Wikipedia)
This method of pushing and popping elements from a stack is also known as “last in, first out” (or LIFO), which is just how it sounds – push an element (like a plate) onto the stack and pop the last element from the top of the stack. You may also find it called “first in, last out” (FILO) in some places.
As we said earlier in the blog, the HP 35S calculator uses an operational stack along with an RPN method of solving mathematical expressions written with infix notation, and those two elements were necessary parts of the solution I implemented for our designers.
So how does one parse infix notation so that the RPN and operational stack can computationally simulate an HP 35S calculator?
Shunting Yard
This is where the brilliance of Edsger Dijkstra’s shunting yard algorithm enters the story. Shunting yards (also known as marshaling yards) are railway systems that enable operators to separate and reassemble freight trains. So if you think about a mathematical expression written with infix notation as a train, you can imagine every character of the expression being a single car. So a shunting yard would separate every element (or train car) from the infix notation train into separate stacks only to later reassemble the elements into a postfix (or RPN) train for computational purposes.
And for Demon Crush’s math system, shunting yard lays at its heart because all a designer wants to type is something like a*(b+c) to get a single output that the game loop can use for gameplay events, like opening locked doors (to learn more about how doors play a big role in our level design, read our blog about keys).

A screenshot from Demon Crush during alpha testing of Kenzo approaching a locked door.
Bringing it all together, after the gameplay system inputs a string into the math system, the system separates an input string like a*(b+c) and parses it into a tokenized character array like the following image.
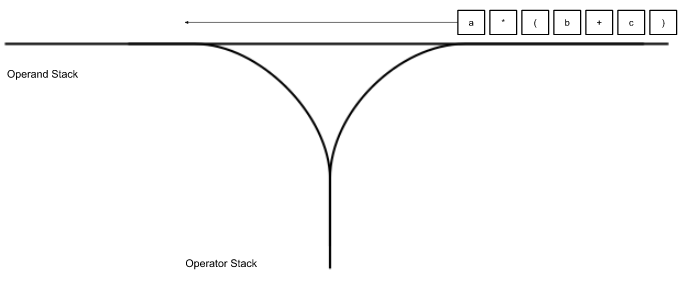
“a” gets pushed to the operand stack
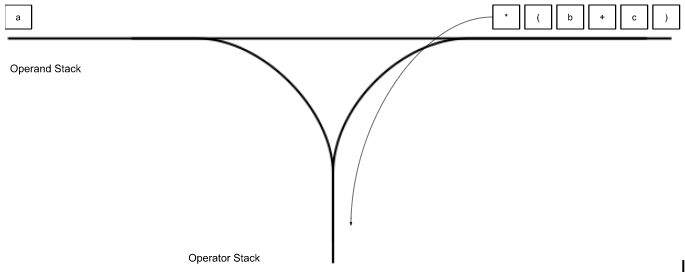
“*” (multiply) gets pushed to the operator stack
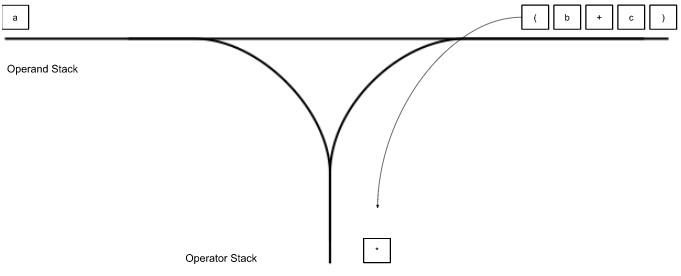
“(” gets pushed to the operator stack
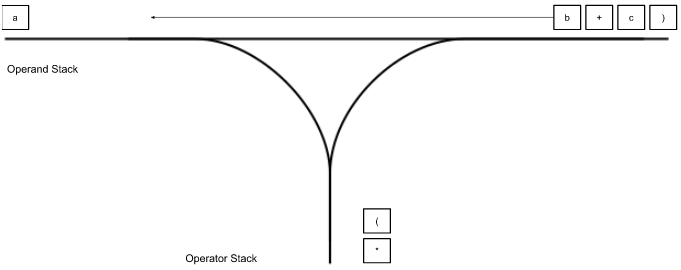
“b” gets pushed to the operand stack
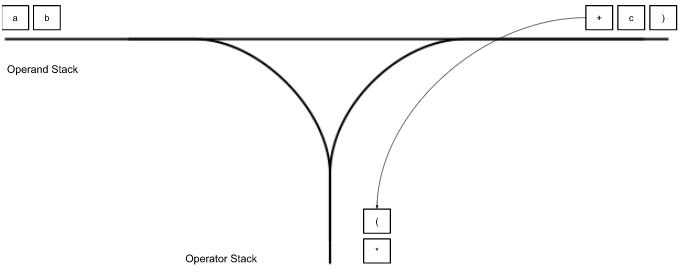
“+” gets pushed to the operator stack
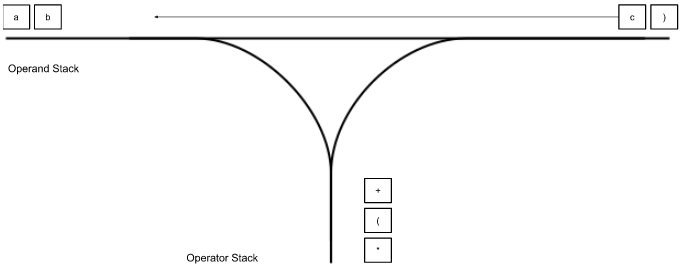
“c” gets pushed to the operand stack
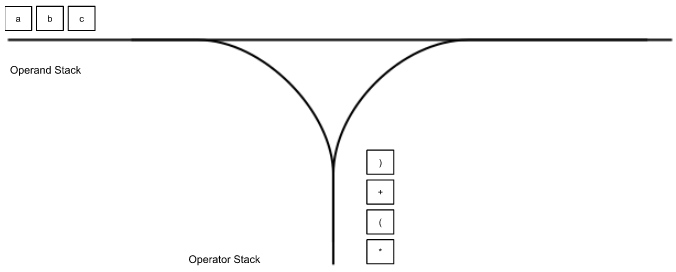
“)” gets pushed to the operator stack
To account for special cases, like the input of logical expressions such as x>y, our implementation of the shunting yard method includes some general operator precedence routines that require our RPN calculator to operate on a single stack that is assembled during the computation of a single result.

At a very high level, the ) character informs logic in our RPN calculator that it needs to perform a computation before finding a ( character, which means that bc+ gets computed before being multiplied with a, such that the final output looks like a*bc+.
What’s cool about this math system is that it can take any mathematical expression input that is represented with infix notation and output a single result to gameplay logic that makes use of RPN output in real-time.
Gameplay Features
We use the system to enable the following gameplay features:
- Key Management
 We use game variables to keep track of which keys Kenzo currently has in his possession. Certain doors can check to see if a game variable has a positive value. For special keys that can be used many times on the correct type of lock, we stop there, but we can also use the system to remove single-use generic keys. Since the game variables are available globally, this also means the HUD can use them to display your current keys next to the health bar.
We use game variables to keep track of which keys Kenzo currently has in his possession. Certain doors can check to see if a game variable has a positive value. For special keys that can be used many times on the correct type of lock, we stop there, but we can also use the system to remove single-use generic keys. Since the game variables are available globally, this also means the HUD can use them to display your current keys next to the health bar. - Combat Damage Adjustment
 Different attacks can do variable damage. Nezumo follows up a successful counter attack with a kick that sends his enemies flying. The kick deals extra damage, but we make sure that the kick is never a killing blow by changing its damage based on the target’s remaining health. We also use dynamic damage modification to make certain traps or weapons lethal against some characters, but not others.
Different attacks can do variable damage. Nezumo follows up a successful counter attack with a kick that sends his enemies flying. The kick deals extra damage, but we make sure that the kick is never a killing blow by changing its damage based on the target’s remaining health. We also use dynamic damage modification to make certain traps or weapons lethal against some characters, but not others. - Cross-Level Events, Doors, and Switches
 Because the game variables that tie into the Demon Crush math system are not bound to any specific level, we can build game events in one level that affect events anywhere else in the game. For example, if Kenzo opens doors and extends bridges to help his allies pass through one area, he may receive their support in places they couldn’t otherwise reach. Or, if Kenzo defeats the commander of an enemy force, we can make soldiers from that force deal less damage and appear in smaller numbers afterward. Even finding the commander can be a function of time, since we can use game variables to decide where to spawn a given enemy.
Because the game variables that tie into the Demon Crush math system are not bound to any specific level, we can build game events in one level that affect events anywhere else in the game. For example, if Kenzo opens doors and extends bridges to help his allies pass through one area, he may receive their support in places they couldn’t otherwise reach. Or, if Kenzo defeats the commander of an enemy force, we can make soldiers from that force deal less damage and appear in smaller numbers afterward. Even finding the commander can be a function of time, since we can use game variables to decide where to spawn a given enemy.
0 Comments